En términos generales, la trigonometría es el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
 |
INDICE
- TEOREMA DE PITAGORA
- FUNCIONES TRIGONOMÉTRICAS
- DETERMINACIÓN DE ÁNGULOS
- FUNCIONES TRIGONOMÉTRICAS
- SUS ÁNGULOS
- PROBLEMAS RESUELTOS
- PROBLEMAS PARA QUE USTED PRACTIQUE RESOLVIÉNDOLOS
- LANZAMIENTO DE PROYECTIL
- FORMULAS
MATEMÁTICA ES FÁCIL SEGÚN EL PUNTO DE VISTA QUE TU LE DES AHORA VEREMOS ¿QUIEN FUE PITAGORA ?,¿CUAL ES EL TEOREMA DE PITAGORA? ¿ PARA QUE SIRVE ESTA FORMULA?
Pitagora: fue un filósofo y matemático griego considerado el primer matemático puro. Contribuyó de manera significativa en el avance de la matemática helénica, la geometría y la aritmética, derivadas particularmente de las relaciones numéricas, y aplicadas por ejemplo a la teoría de pesos y medidas, a la teoría de la música o a la astronomía. Es el fundador de la Hermandad Pitagórica, una sociedad que, si bien era de naturaleza predominantemente religiosa, se interesaba también en medicina, cosmogonía, filosofía, ética y política, entre otras disciplinas. El rigorismo formuló principios que influyeron tanto en Platón como en Aristóteles y, de manera más general, en el desarrollo de la matemática y en la filosofía racional en Occidente.
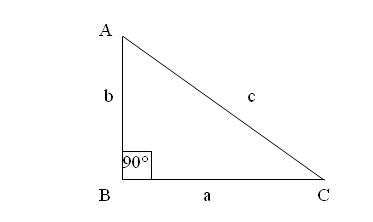
LA FORMULA ES:
h2 = + a2 = b2
hipotenusa al cuadrado es igual a las suma de sus catetos al cuadrado.
El cateto A es también llamado cateto ayasente
El cateto B encamobio es llamado opuesto
Con este vídeo sera mas fácil para que usted pueda entender mucho mejor como se puede encontrar la hipotenusa:
El cateto A es también llamado cateto ayasente
El cateto B encamobio es llamado opuesto
Con este vídeo sera mas fácil para que usted pueda entender mucho mejor como se puede encontrar la hipotenusa:
Esta formula te ayudara a encontrar el lado mas grande del triangulo rectángulo osea la hipotenusa como también el seno coseno y tangente que son funcione trigonométricas
Para las Funciones Trigonométricas, como se mencionó anteriormente,
haremos uso del Teorema de Pitágoras y trabajaremos con las Funciones
de Seno, Coseno y Tangente, y sus inversas, además de apoyarnos
siempre con la Calculadora.
FUNCIÓN SENO.
FUNCIÓN COSENO
FUNCIÓN TANGENTE
FUNCIÓN COTANGENTE
FUNCIÓN SECANTE
FUNCIÓN COSECANTE
con estas formulas tu vas a poder sacar las siguientes funciones ahora con un vídeo te lo voy a especificar
siempre tienes que ver que la trigonométrica no es difícil solo debes aplicarte mucho mas y tendrás un aprendizaje mas rápido y productivo
Por medio de la calculadora te puedes ayudar a sacare las funciones aquí te dejo este vídeo:
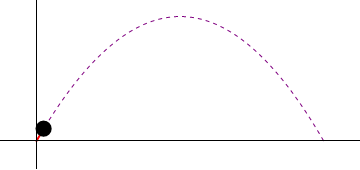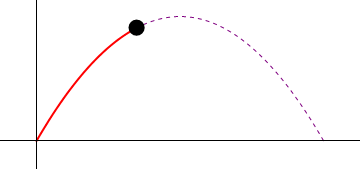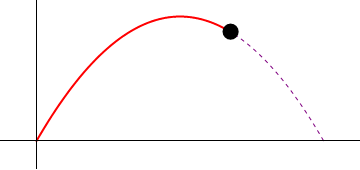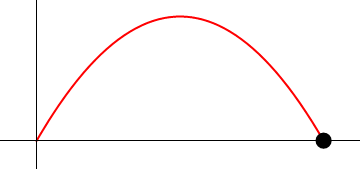AQUÍ TU PODRÁS OBSERVAR EL MOVIMIENTO DEL PROYECTIL....
EJEMPLOS DE PROBLEMAS DE TRIGONOMÉTRICA
tonemos en la vida distintos ejemplos de una proyección de un triangulo rectángulo aquí tu te darás cuenta de o que te digo espero que algunos de mis ejercicios te ayude a entender mejor
2 ejemplo
Un proyectil es cualquier objeto lanzado en el espacio por la acción de una fuerza. Aunque un balón arrojado es también un proyectil técnicamente, el término se refiere generalmente a un arma.1 2 Para los detalles matemáticos referentes a la trayectoria de un proyectil, véase ecuaciones de movimiento.
AQUÍ TU PODRÁS OBSERVAR EL MOVIMIENTO DEL PROYECTIL....
Ejemplo del cazador
Un cazador ve que un chango se encuentra a una distancia horizontal xc y una altura yc, medidas desde la posición del cazador. Suponga que el cazador le dispara al chango una flecha con una velocidad inicial a un cierto ángulo. ¿Cuál es el valor mínimo de la velocidad inicial de la flecha y el valor del ángulo de disparo para que el cazador de en el blanco?
Respuesta: Para obtener el ángulo de disparo es necesario utilizar la ecuación (1.5). Considerando que x0 = y0 = 0, y que la flecha tiene que pasar por la posición donde se localiza el chango (xc, yc) la ecuación para obtener el ángulo de disparo es
La solución de esta ecuación nos permite calcular el ángulo de disparo. Escribiendo la ecuación anterior de la siguiente manera
se encuentra que tiene la forma 
y la solución se obtiene mediante la fórmula 
. Utilizándola, se obtiene
y la solución se obtiene mediante la fórmula . Utilizándola, se obtiene
Cuando el discriminante de esta última ecuación se iguala a cero, se obtiene el valor mínimo de la velocidad del proyectil. Haciéndolo, se obtiene la ecuación para la velocidad
Utilizando la misma fórmula para resolver ecuaciones de segundo grado, se obtiene que
. La solución que se apega a la situación de los proyectiles es la asociada al signo positivo y entonces la velocidad mínima del proyectil es
. La solución que se apega a la situación de los proyectiles es la asociada al signo positivo y entonces la velocidad mínima del proyectil es
Combinando la ecuación (1.9) y la ecuación (1.7), se encuentra que el ángulo de disparo asociado a la velocidad mínima del proyectil esta dado por
